Игры начали привлекать внимание специалистов по программированию компьютеров задолго до того, как в середине 50-х годов сотрудник Станфордского университета Джон Маккарти предложил называть область, связанную с таким программированием, искусственным интеллектом. Любопытно, что еще на заре вычислительной техники некоторые из ее пионеров утверждали, что даже скептики будут вынуждены признать интеллектуальные способности машины, когда она научится прилично играть в шахматы. Именно тогда обрела популярность идея разработки программы, способной достаточно хорошо играть в шахматы. Замысел создания механического шахматиста на целый век опередил появление компьютеров. В начале XIX в. всеобщее изумление вызвал шахматный автомат, изобретенный Иоганном Непомуком Мейзелем. Интеллект этой машины, увы, оказался совершенно «естественным»: в шахматы играл человек, скрытый в автомате. Позднее, в 1894 г., в одном из первых научно-фантастических произведений (рассказе А. Бирса «Хозяин Моксона») фигурировал робот-шахматист, который так часто проигрывал, что в конце концов — при очередном поставленном ему мате — убил своего творца.

В кабине космического корабля астронавт будущего коротает время в компании робота, играя с ним в карты. Кадр из фильма «Безмолвная работа».

Привлекательность игр, и прежде всего шахмат, для специалистов по ИИ совершенно очевидна. Бесспорно, что играющая в шахматы машина должна обладать высоким уровнем интеллекта. Ведь большинство из нас воспринимают шахматного гроссмейстера как воплощение интеллекта. Однако в играх интеллект проявляется ограниченно, ибо здесь он направлен на решение вполне определенных задач. Поэтому нетрудно найти такие способы кодирования состояния игры (положения отдельных фигур в любой момент ее), которыми может оперировать компьютер. Правила игры ясны и четки. В программе не требуется учитывать такие факторы, как удача или обман. Оптимальный ход можно найти исключительно на основе логических рассуждений, по крайней мере теоретически. Таким образом, компьютер можно легко научить разбираться в текущей позиции и на основе определенных формальных правил предвидеть ситуации, которые могут естественно сложиться после очередного хода. Единственное, чем нужно вооружить машину для такого анализа, — это алгоритм.
Термин «алгоритм» весьма распространен в теории вычислительной техники. Он означает не что иное, как совокупность строго определенных правил работы компьютера или мышления человека. В арифметике, например, мы пользуемся алгоритмами (правилами) сложения, вычитания, деления и умножения чисел. Если обратиться, скажем, к кулинарии, то здесь перечень исходных продуктов, с которого начинается описание каждого рецепта, можно рассматривать как исходные данные, а следующие за ним инструкции по приготовлению — как алгоритм преобразования этих продуктов в конкретное кушанье. В области ИИ, как и в других областях программирования компьютеров, алгоритм составляет основу основ. Приступая к формальному написанию программы, программист должен четко представлять весь путь решения поставленной задачи. В случае шахмат или других аналогичных игр, например шашек, основной алгоритм носит название дерева решений.
Ключ к успеху в игре, безусловно, скрыт в способности видеть ситуацию на несколько ходов вперед; это позволяет рассчитать, к чему может привести очередной ход. Выигрыша добивается тот игрок, который может дальше своего соперника довести последовательность рассуждений типа «...если я сделаю ход А, то он может ответить ходом В, С или D; если он сделает ход С, то я буду вынужден предпринять ход Н, I или J и т. д.» Такой процесс рассуждений начинается с определенного момента в игре, схематически представляемого как некий «узел» с отрезками, отходящими от него к другим узлам, каждый из которых соответствует положению в игре, возникающему после конкретного хода. В свою очередь от каждого из этих узлов отходят линии, ведущие к другим узлам, которые соответствуют состояниям, возникающим в игре при ответных ходах соперника.
Теоретически такое дерево можно построить начиная с исходного состояния, т. е. с положения фигур до начала игры, а завершать его будет узел, представляющий состояние игры в момент ее окончания. Однако на практике построение подобного дерева превосходит возможности любого самого крупного компьютера, какой только можно представить. Даже в такой простейшей игре, как «крестики — нолики», где начальное состояние и конечный узел (соответствующий моменту, когда все девять клеток заполнены крестиками и ноликами) отделены друг от друга всего девятью шагами, или уровнями, полное дерево решений будет насчитывать по меньшей мере 60 тыс. ветвей, или узлов. А в случае шахмат после сравнительно небольшого числа ходов дерево решений разрастется до неуправляемых масштабов. Этот результат есть не что иное, как просто другой способ выразить тот весьма известный факт, что число позиций на доске или число состояний, которые могут возникнуть в шахматной партии, бесконечно велико. Отсюда следует, что еще до перехода к последним стадиям эндшпиля шахматная программа не в состоянии прогнозировать развитие партии на такое число ходов, которое позволило бы ей «увидеть» положение, в котором достигается победа. Следовательно, в подобной ситуации само по себе наличие алгоритма, основанного на анализе дерева решений, явно недостаточно.
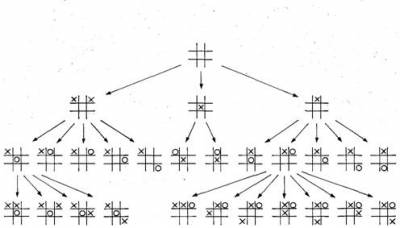
Дерево решений. Здесь дерево решений представлено в том виде, в каком его может построить программа, играющая в «крестики—нолики». На самом верхнем уровне имеется всего один «узел» (1), который соответствует начальному состоянию игры; он имеет вид пустой сетки из девяти квадратов. В этом начальном состоянии машина может сделать один из трех ходов (2). (Поскольку на этой стадии игры ячейки сетки симметричны, многие из возможных ходов эквивалентны; они обозначены синим.) Начиная с одного из трех узлов на уровне 2, противник машины может ответить одним из 12 возможных ходов — они и составляют уровень 3. На этом этапе дерево решений разрастается настолько широко, что отобразить его здесь во всей полноте уже невозможно; поэтому на уровне 4 показаны только 11 и? 60 с лишним возможных состояний, из которых машина может сделать свой второй ход. Отметим, что даже для такой элементарной игры, как «крестики—нолики», ко времени достижения конечного, девятого, уровня полное дерево решений насчитывает уже более 60 тыс. ветвей, каждая из которых соответствует одному из возможных состояний игры.
Выход из этого положения состоит в использовании либо каких-то средств, ограничивающих диапазон исследуемых (или искомых) ситуаций, либо какой-то системы, позволяющей присваивать значения предсказываемым состояниям, которые отмечены узлами на периферии дерева решений. В программах, играющих в шахматы, используются совместно оба этих подхода. Как правило, такие программы строят дерево решений, которое позволяет исследовать лишь ограниченную область доски, например стратегически важный центр или области расположения ключевых фигур, и обращаются к другим областям лишь в тех случаях, когда начальный поиск не приводит к решению, обещающему благоприятное развитие партии. Если найден потенциально хороший ход, то может быть предпринят более глубокий поиск с целью изучения возможностей — без выхода из выбранной перспективной области, а лишь путем просмотра большего числа ходов. Если поиск в какой-то области доски достаточно быстро показывает, что все возможные ходы ведут к проигрышу, то поиск здесь можно сразу прекратить, переключившись на изучение других областей.
Но даже при таких методах ограничения размеров исследуемых деревьев решений (т. е. при отсечении отдельных ветвей) потребуется ввести некоторую систему счета, позволяющую машине оценивать конечные состояния дерева и решать, какие из них можно считать «хорошими», а какие — «плохими». Другими словами, машина должна располагать рядом эмпирических правил на тот случай, если в своем поиске она зайдет настолько далеко, насколько позволят ее ресурсы. Такие правила должны говорить машине примерно следующее: «Достижение этого состояния в игре ведет к успеху» или «Если в игре сложится данная ситуация, то твое будущее бесперспективно».
Правила такого рода, используемые во всех системах ИИ, называются эвристиками. Они сродни различного рода догадкам, инстинктивно найденным тактическим и стратегическим приемам, а также интуитивным, основанным на опыте решениям, которыми широко пользуются люди во время игры. Но как вооружить машину такими правилами? Разумеется, некоторые фундаментальные и относительно простые эвристики можно ввести в программу в «готовом виде». Однако программа, использующая только такие предварительно заготовленные суждения, никогда не сможет добиться успеха в сложной, замысловатой игре, так как опытный противник-человек быстро разберется в ее нехитрой логике.
Наиболее интересный аспект игровых программ связан с использованием методов, позволяющих машине совершенствовать и пересматривать имеющиеся эвристики или даже изобретать новые. Одним из первых обратился к изучению этой возможности американец А. Л. Сэмюэль, который в конце 50-х годов составил программу, играющую в шашки. Хотя вследствие значительно большей сложности шахмат методы Сэмюэля во всей их полноте к ним неприменимы, тем не менее все современные программы игры в шахматы разработаны на основе весьма сходных принципов.
Существенная особенность данного подхода заключается в том, что программа должна иметь возможность накапливать собственный опыт. Вооруженная сначала базовым набором эвристик программа играет ряд партий с людьми (интересно отметить, что машины не в состоянии обучаться, играя друг с другом, поскольку они снабжены одинаковыми наборами эвристик и развитие их партии предопределено заранее). Если машина проиграет, то она анализирует партию, выявляя позиции, которые оказались плохими в свете ее нового опыта (хотя на основе базовых эвристик она оценивала их как удачные). Если же машина выиграет (даже будучи в положении, которое по тем же эвристикам оценивалось как слабое), то она пересматривает свои правила, корректируя их. Со временем, анализируя раз за разом результаты своих шахматных сражений с людьми, машина переработает имеющиеся у нее эвристики до такой степени, что их, пожалуй, теперь правильнее будет назвать продуктом ее собственного опыта, нежели исходным набором правил, заложенных в нее сначала. Сказанное отнюдь не означает, что каждый компьютер-шахматист должен проходить этот трудоемкий процесс тренировки: если программа доведена до требуемого стандарта, ее просто можно копировать в нужном количестве.
Еще до того как Сэмюэль разработал свои методы обучения машин, на практике уже использовался фундаментальный метод ведения поиска по дереву решений. Этот так называемый минимаксный метод был изобретен Клодом Шенноном, одним из основоположников кибернетики. Нетрудно понять, что машине абсолютно ничего не даст простой просмотр нижнего уровня дерева решений, т. е. узлов с числовыми оценками, представляющими все состояния игры (считая от текущей позиции), которые система еще способна предвидеть. Попытка машины проследить последовательность ходов, ведущую к узлу с наивысшей числовой оценкой, ни к чему не приведет. Выбор такого метода был бы равносилен предположению, что каждый свой новый ход противник делает оптимальным не для себя, а для машины. Благоразумнее, однако, предположить, что противник всегда выбирает тот ход, который наименее выгоден машине. Именно на этом принципе и основан минимаксный метод.
Он заключается в следующем. Начиная с уровня, который содержит всего один узел, соответствующий состоянию игры в тот момент, когда очередной ход должна делать машина, строится дерево решений заданной глубины. Конечный уровень всегда выбирается так, что очередной ход снова принадлежит машине, т. е. уровень 3, уровень 5, уровень 7 и т. д. (Если предусмотрена возможность перестройки машины на игру с различной степенью мастерства, то установка ее в режим более высокого класса игры приводит к построению дерева решений, которое обеспечивает обзор на дополнительные два, четыре или шесть уровней вперед.) Используя свои эвристики, машина затем производит числовую оценку узлов только конечного уровня, игнорируя узлы всех промежуточных уровней независимо от того, представляют они ее собственные ходы или ходы противника.
Минимаксный алгоритм. Этот базовый алгоритм основан на предположении, что, делая свой ход, машина всегда будет пытаться максимизировать набранные ею очки, тогда как ее противник при каждом ходе, напротив, будет стараться минимизировать набранные машиной очки. Чтобы решить, какой из двух возможных ходов лучшее машина делает предварительный просмотр на столько шагов вперед, на сколько позволяют ее ресурсы (в нашем упрощенном примере такой просмотр производится до уровня 5). Машина присваивает числовые оценки, или очки, каждому узлу конечного уровня просмотра; на схеме эти узлы сгруппированы в пары — каждая пара получилась из узла предшествующего уровня 4. Предположив, что она делает наилучший ход, машина переносит более высокую числовую оценку каждой рассматриваемой пары исходов на порождающий ее узел на уровне 4. После этого она переносит минимальную оценку каждой пары уровня 4 на уровень 3, по существу действуя в предположении, что противник всегда будет пытаться минимизировать ее потенциальные очки. В результате такой минимаксной процедуры машина определяет наиболее выгодную для нее последовательность ходов (красная ломаная линия, идущая снизу вверх).
Машина «Чесе чэлленджер» для игры в шахматы, изготовленная фирмой Фидели™ электронике». По своему мастерству она значительно уступает человеку-гроссмейстеру.
Теперь машина должна просмотреть числовые оценки узлов конечного уровня, чтобы установить, какой из узлов представляет то оптимальное состояние, которое она может достичь в предположении, что ее противник будет по возможности препятствовать осуществлению ее намерений. Как видно из приведенной схемы, числовые оценки объединяются в группы, причем каждая группа узлов представляет возможные состояния, которые могут возникнуть в результате одного из ходов противника на предыдущем уровне. Из каждой такой группы машина выбирает узел с наивысшей, т. е. максимальной, оценкой, исходя из предположения, что она сделает наилучший ход. Затем машина переносит эту оценку «назад», на узел, расположенный на предшествующем, более высоком уровне; из этого меньшего набора узлов с перенесенными снизу числовыми оценками программа выбирает наихудшую, или минимальную, числовую оценку, исходя из предположения, что ее противник сделает все возможное, чтобы свести ее оценку к минимуму. Процесс продолжается до тех пор, пока в результате такого движения в обратном направлении программа не дойдет до уровня 1; линия, вдоль которой эта последняя числовая оценка переносилась снизу вверх, представляет последовательность наилучших ходов машины. Обратная трассировка на основе использования минимаксной процедуры — операция, требующая много времени даже для компьютера, поскольку при ее проведении машина должна проходить отдельно по каждой ветви дерева решений. Были разработаны различные приемы, ускоряющие отдельные процессы поиска. Наиболее известна среди этих приемов процедура альфа-бета. Хотя математически она весьма сложна, в ее основе лежит довольно простая идея, которая сводится к следующему. Если в ходе обратной трассировки по какой-либо ветви обнаруживается, что максимум или минимум на некотором уровне уступает по оценкам соответствующим показателям на том же уровне для уже пройденных ветвей, то поиск по этой ветви прекращается.
Свидетельством значительных достижений в развитии данной области ИИ может служить тот факт, что машины, способные играть в шахматы, выпускаются теперь серийно. Существует, однако, мнение, что интеллект компьютера, играющего в шахматы, и интеллект, шахматиста-человека — далеко не одно и то же, Слушая рассказы гроссмейстеров о сыгранных партиях, их мотивировки того или иного хода, знакомясь с их стратегией и тактикой, невольно приходишь к мысли, что мышление человека-шахматиста отличается большей тонкостью, оно более подвластно интуиции и в меньшей степени той строгой, но ограниченной логике, которой легко можно обучить машину. Различие между механизмом мышления человека, все еще сохраняющим свою загадочность, и «мыслительными способностями» машины становится очевидным, если обратиться ко второй области приложения искусственного интеллекта — решению задач.